Algorithm | DFS & BFS

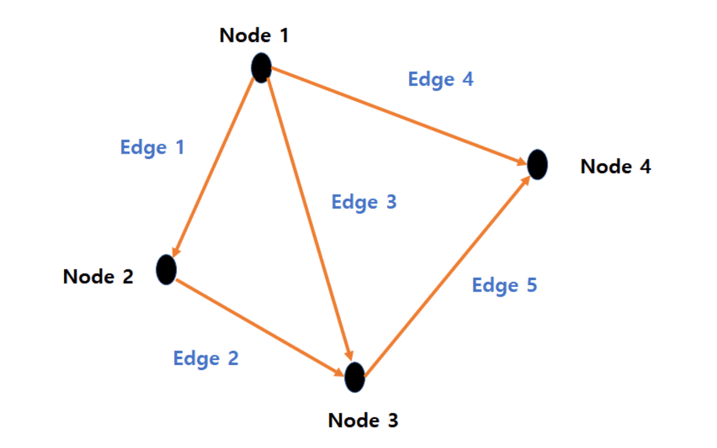
DFS(Depth-First Search) 깊이 우선 탐색, BFS(Breadth-First Search) 너비 우선 탐색 모두 graph를 탐색하는 방법이다. 알고리즘에서 graph란, node와 그 node를 연결하는 edge로 이루어진 자료구조를 말하며, 이를 탐색한다는 것은 하나의 node에서 시작해 edge로 연결된 차례대로 모든 node를 한번씩 방문하는 것을 말한다.

Node와 Edge로 구성된 Graph

Depth-First Search (DFS: 깊이 우선 탐색)

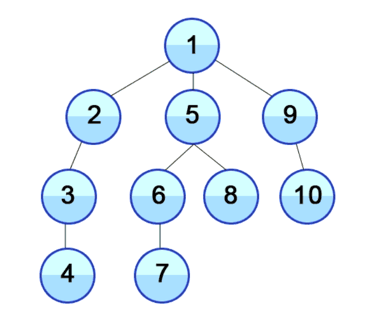
DFS는 탐색 graph의 최초의 node를 확장하여 목표 상태가 발견될 때까지 더 깊이 확장하는 맹목적 탐색 (Blind search)이다. 만일 자식node를 갖고 있지 않은 node에 이르면 back-tracking하여 다음 node에서 출발한다. 즉, 시작점 부터 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하고 넘어가는 방법이다.
DFS는 다음과 같은 몇가지 특징을 가진다

• 자기 자신을 호출하는 순환 알고리즘 형태를 가진다
• 전위순회를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다
• 단순 검색 속도는 너비 우선 탐색(BFS) 보다 느림
• 구현 시 graph탐색의 경우 어떤 node를 방문했었는지 여부를 반드시 검사해야 한다 (그렇지 않을 경우 무한루프 주의!)
• Recursion 또는 Stack을 이용하여 구현 가능하다

DFS의 시간 복잡도

• 인접 리스트로 표현된 그래프: O(N+E)
• 인접 행렬로 표현된 그래프: O(N^2)
• 그래프 내에 적은 숫자의 간선(edge)만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다.

Breadth-First Search (BFS: 너비 우선 탐색)

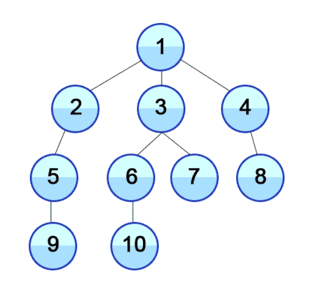
BFS란 너비 우선 탐색이라고도 불리며 graph에서 시작 node에 인접한 node부터 탐색하는 알고리즘이다. 시작 node로부터 가까운 node 먼저 방문하고 멀리 떨어져 있는 node를 나중에 방문하는 방식으로 순회함으로써 노드를 넓게(wide) 탐색한다. 주로 두 node 사이의 최단 경로 혹은 임의의 경로를 찾고 싶을 때 이 방법을 사용한다. BFS는 다음의 특징을 가진다

• 직관적이지 않다는 단점이 있다

• 재귀적으로 동작하지 않는다

• 구현시 어떤 node를 방문했었는지 여부를 반드시 검사해야 한다

• Queue를 이용하여 구현가능하다

• Prime algorithm(프림 알고리즘), Dijkstra algorithm(다익스트라 알고리즘)과 유사하다

BFS의 시간 복잡도

• 인접 리스트로 표현된 그래프: O(N+E)
• 인접 행렬로 표현된 그래프: O(N^2)
• 깊이 우선 탐색(DFS)과 마찬가지로 그래프 내에 적은 숫자의 간선(edge)만을 가지는 희소 그래프(Sparse Graph) 의 경우 인접 행렬보다 인접 리스트를 사용하는 것이 유리하다

구현예제

const graph = {
  A: ["B", "C"],       B: ["A", "D"],   C: ["A", "E"],
  D: ["B", "F"],       E: ["C", "G"],   F: ["D", "H", "I"],
  G: ["E", "J", "K"],  H: ["F", "L"],   I: ["F", "M"],
  J: ["G", "N"],       K: ["G", "O"],   L: ["H"],
  M: ["I", "P"],       N: ["J"],        O: ["K"],
  P: ["M"]
};

DFS(깊이우선탐색)

const dfs = (graph, start) => {

    const checked = [];    // 탐색 완료 데이터
    const willCheck = [];  // 탐색 예정 데이터
    
    willCheck.push(start);
    
    while(willCheck.length!==0){
      const node = willCheck.pop();  // 스택(Last In First Out)
      if(!checked.includes(node)){
            checked.push(node);
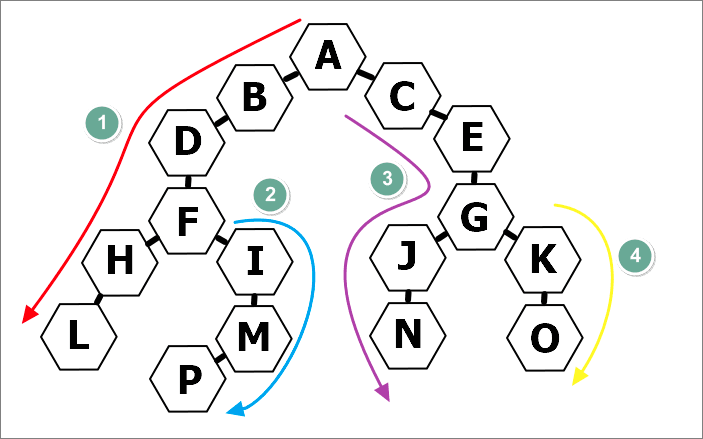
         //reverse() 제거 시 그림의 4,3,2,1 순서로 탐색     
           willCheck.push(...graph[node].reverse());  
        
      }
   }
    return checked;
}

console.log(dfs(graph, "A"));
// ['A', 'B', 'D', 'F', 'H', 'L', 'I', 'M', 'P', 'C', 'E', 'G', 'J', 'N', 'K', 'O']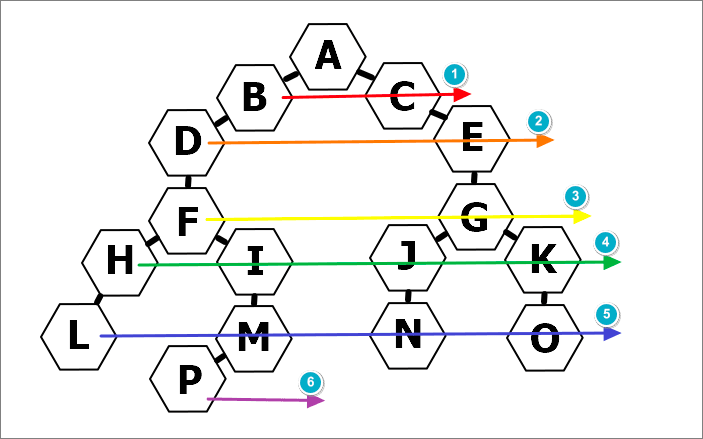

BFS(너비우선탐색)

const bfs = (graph, start) => {
  const checked = [];
  const willCheck = [];

  willCheck.push(start);

  while(willCheck.length!==0){
    const node = willCheck.shift(); // 큐(First In First Out)
    if(!checked.includes(node)){
      checked.push(node);
      willCheck.push(...graph[node]);
    }
  }
  return checked;
}
console.log(bfs(graph, "A"));
// ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J', 'K', 'L', 'M', 'N', 'O', 'P']